Materi matematika kuartil membahas tentang cara memahami dan menghitung kuartil dalam suatu data. Kuartil merupakan nilai yang membagi data yang telah diurutkan menjadi empat bagian yang sama besar. Pemahaman tentang kuartil sangat penting dalam menganalisis dan menginterpretasikan data statistik, membantu dalam memahami sebaran dan karakteristik data.
Materi ini akan membahas definisi, jenis-jenis, rumus perhitungan, interpretasi, dan penerapan kuartil dalam berbagai konteks matematika, mulai dari data tunggal hingga data berkelompok. Selain itu, akan dibahas juga contoh-contoh soal dan latihan untuk memperdalam pemahaman.
Definisi Kuartil
Kuartil merupakan nilai yang membagi data yang telah diurutkan menjadi empat bagian yang sama besar. Pemahaman tentang kuartil sangat penting dalam analisis data, karena memberikan gambaran mengenai sebaran data dan membantu dalam mengidentifikasi nilai tengah dari data.
Definisi Matematika Kuartil
Secara matematis, kuartil adalah nilai-nilai yang membagi data yang telah diurutkan menjadi empat bagian yang sama. Kuartil pertama (Q1) adalah nilai yang berada di posisi 25% dari data, kuartil kedua (Q2) adalah nilai median (50% dari data), dan kuartil ketiga (Q3) adalah nilai yang berada di posisi 75% dari data. Rumus perhitungan kuartil dapat bervariasi tergantung pada jumlah data dan apakah datanya ganjil atau genap.
Arti Penting Kuartil dalam Statistika
Kuartil memberikan informasi yang lebih komprehensif tentang distribusi data dibandingkan dengan mean atau median saja. Hal ini karena kuartil mempertimbangkan sebaran data secara lebih detail, bukan hanya nilai tengahnya. Dengan mengetahui kuartil, kita dapat memahami rentang data, keberadaan outlier, dan bentuk distribusi data.
Perbandingan Kuartil, Median, dan Mean
| Statistik | Definisi | Penjelasan |
|---|---|---|
| Kuartil | Nilai yang membagi data terurut menjadi empat bagian sama besar. | Memberikan gambaran lebih rinci tentang sebaran data. |
| Median | Nilai tengah dari data yang telah diurutkan. | Memberikan gambaran nilai tengah dari data. |
| Mean | Rata-rata dari seluruh data. | Memberikan gambaran nilai rata-rata dari data. |
Hubungan Kuartil dengan Distribusi Data
Kuartil sangat berkaitan erat dengan distribusi data. Distribusi yang simetris akan memiliki Q1, median, dan Q3 yang berjarak sama. Jika distribusi miring ke kanan, Q3 akan lebih jauh dari median dibandingkan Q1. Sebaliknya, jika distribusi miring ke kiri, Q1 akan lebih jauh dari median dibandingkan Q3. Hal ini membantu dalam memahami bentuk dan pola distribusi data.
Contoh Penerapan Kuartil dalam Kehidupan Sehari-hari
Penerapan kuartil banyak ditemui dalam berbagai bidang. Misalnya, dalam bidang pendidikan, kuartil dapat digunakan untuk menganalisis nilai ujian siswa dan mengidentifikasi sebaran kemampuan. Dalam bisnis, kuartil dapat digunakan untuk menganalisis penjualan produk dan mengidentifikasi produk yang paling laris atau paling kurang diminati. Contoh lain adalah dalam bidang kesehatan, kuartil dapat digunakan untuk menganalisis tinggi badan atau berat badan populasi tertentu.
Jenis-jenis Kuartil
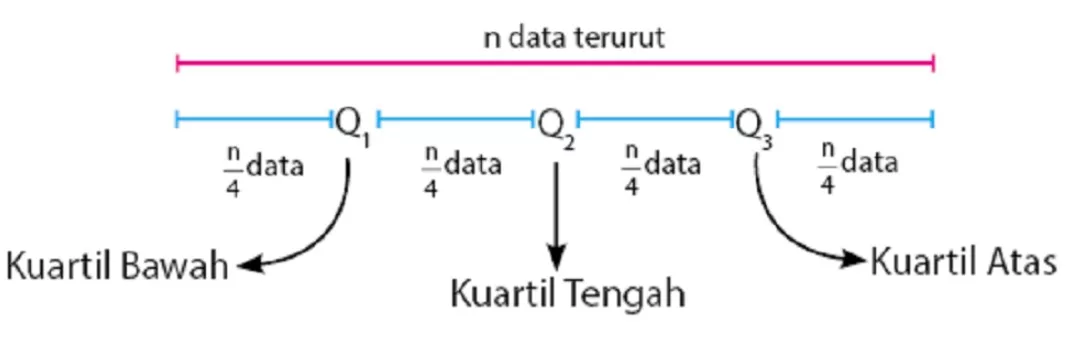
Kuartil merupakan nilai-nilai yang membagi data terurut menjadi empat bagian yang sama besar. Pemahaman tentang jenis-jenis kuartil sangat penting dalam menganalisis distribusi data dan menemukan informasi penting seperti nilai tengah data.
Kuartil Pertama (Q1), Kedua (Q2), dan Ketiga (Q3)
Kuartil pertama (Q1) merupakan nilai yang membagi 25% data terendah dari data terurut. Kuartil kedua (Q2) merupakan nilai tengah dari data terurut, sama dengan median. Kuartil ketiga (Q3) merupakan nilai yang membagi 75% data terendah dari data terurut.
Posisi Kuartil dalam Data Terurut
Berikut tabel yang menunjukkan posisi kuartil dalam data yang terurut:
| Kuartil | Posisi |
|---|---|
| Q1 | (n + 1) / 4 |
| Q2 | (n + 1) / 2 |
| Q3 | 3(n + 1) / 4 |
Dimana ‘n’ adalah jumlah data.
Cara Menghitung Kuartil pada Data Tunggal
Untuk menghitung kuartil pada data tunggal, langkah-langkahnya adalah sebagai berikut:
- Urutkan data dari yang terkecil hingga terbesar.
- Hitung posisi Q1, Q2, dan Q3 menggunakan rumus di atas.
- Jika posisi kuartil adalah bilangan bulat, nilai kuartil tersebut adalah data pada posisi tersebut.
- Jika posisi kuartil adalah bilangan desimal, nilai kuartil dihitung dengan interpolasi.
Perbedaan Penghitungan Kuartil pada Data Tunggal dan Data Berkelompok
Perbedaan utama antara penghitungan kuartil pada data tunggal dan data berkelompok terletak pada cara menentukan nilai data pada posisi tertentu. Pada data tunggal, nilai data langsung diketahui. Sedangkan pada data berkelompok, nilai data pada posisi tertentu harus dihitung menggunakan frekuensi kumulatif.
Pada data berkelompok, kita perlu mencari interval kelas yang memuat kuartil. Kemudian, menggunakan frekuensi kumulatif, kita menghitung nilai kuartil tersebut.
Contoh Menghitung Kuartil pada Data Sederhana
Misalnya, terdapat data berikut: 2, 4, 6, 8, 10. Jumlah data (n) = 5.
- Q1: ((5 + 1) / 4) = 1.5. Q1 berada di antara data ke-1 dan ke-2. Q1 = (2 + 4) / 2 = 3.
- Q2: ((5 + 1) / 2) = 3. Q2 adalah data ke-3, yaitu 6.
- Q3: (3
– (5 + 1) / 4) = 4.5. Q3 berada di antara data ke-4 dan ke-5. Q3 = (8 + 10) / 2 = 9.
Rumus dan Cara Menghitung Kuartil
Setelah memahami konsep dasar kuartil, mari kita pelajari bagaimana menghitungnya. Rumus dan cara perhitungan berbeda untuk data tunggal dan data berkelompok. Pemahaman tentang langkah-langkah perhitungan akan sangat membantu dalam menganalisis data.
Rumus dan Cara Menghitung Kuartil pada Data Tunggal
Untuk data tunggal, urutan data sangat penting. Langkah-langkahnya adalah sebagai berikut:
- Urutkan data dari yang terkecil hingga terbesar.
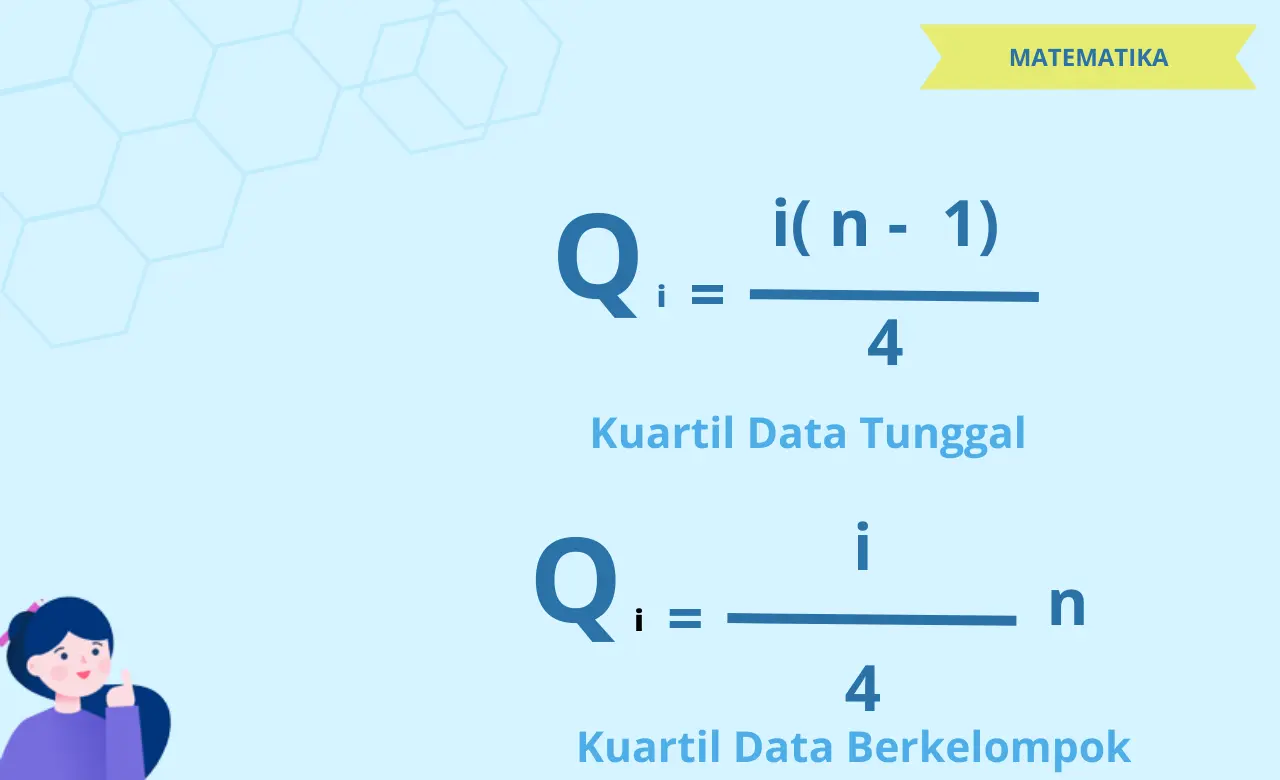
- Tentukan letak kuartil ke-i dengan rumus: Qi = ( i/4)
, di mana i adalah kuartil ke- i (1, 2, atau 3) dan n adalah jumlah data.n
- Jika hasil perhitungan di langkah 2 berupa bilangan bulat, maka kuartil ke- i adalah data pada urutan ke-hasil perhitungan. Jika hasil perhitungan berupa bilangan desimal, maka kuartil ke- i dihitung dengan interpolasi.
Contoh Soal dan Penyelesaian
Misalnya, terdapat data berikut: 5, 8, 10, 12, 15, 18, 20. Jumlah data ( n) adalah 7.
- Urutkan data: 5, 8, 10, 12, 15, 18, 20
- Hitung letak Q1: (1/4)7 = 1.75. Q 1 terletak di urutan ke-2.
- Hitung letak Q 2: (2/4)7 = 3.5. Q 2 terletak di urutan ke-4.
- Hitung letak Q 3: (3/4)7 = 5.25. Q 3 terletak di urutan ke-6.
- Berdasarkan urutan data, Q 1 = 8, Q 2 = 12, dan Q 3 = 18.
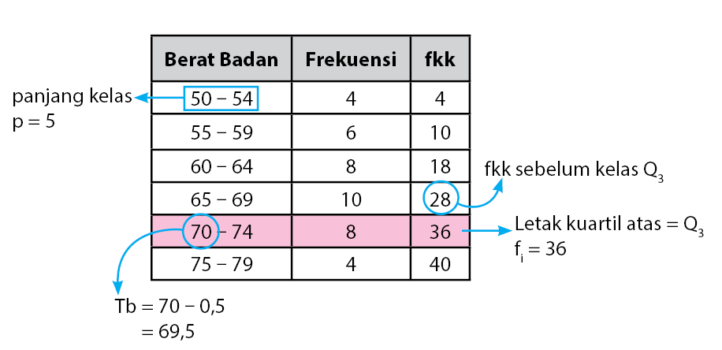
Rumus dan Cara Menghitung Kuartil pada Data Berkelompok
Untuk data berkelompok, dibutuhkan tabel distribusi frekuensi. Berikut langkah-langkah perhitungannya:
| Langkah | Deskripsi |
|---|---|
| 1 | Tentukan kelas interval yang memuat kuartil ke-i. |
| 2 | Hitung nilai kumulatif frekuensi sebelum kelas interval tersebut. |
| 3 | Gunakan rumus: Qi = Lb + ((i/4)
c
|
Menentukan Kuartil pada Data dengan Nilai Ekstrim
Nilai ekstrim (sangat besar atau sangat kecil) dapat memengaruhi perhitungan kuartil. Untuk mengatasi hal ini, perlu dipertimbangkan pengaruh nilai-nilai tersebut pada data dan interpretasi hasilnya.
Menghitung Kuartil pada Data Berkelompok dengan Frekuensi
Untuk data berkelompok dengan frekuensi, langkah-langkahnya sama seperti pada data berkelompok, tetapi perlu memperhatikan frekuensi setiap kelas interval dalam perhitungan.
Interpretasi Nilai Kuartil
Memahami nilai kuartil sangat penting untuk menginterpretasikan penyebaran data. Kuartil membagi data terurut menjadi empat bagian yang sama besar, memberikan gambaran mengenai sebaran data dan posisi relatif data di dalam himpunan data.
Interpretasi Kuartil Pertama (Q1)
Kuartil pertama (Q1) merepresentasikan nilai data yang berada di posisi 25% dari data terurut. Artinya, 25% data berada di bawah Q1. Nilai ini memberikan gambaran tentang batas bawah dari 25% data terendah. Semakin rendah nilai Q1, semakin rendah rata-rata data dalam kelompok data tersebut.
Makna Kuartil Kedua (Q2) sebagai Median, Materi matematika kuartil
Kuartil kedua (Q2) identik dengan median. Median merupakan nilai tengah dari data terurut. Dengan demikian, 50% data berada di bawah Q2 dan 50% data berada di atas Q2. Q2 memberikan gambaran tentang titik tengah data dan memberikan informasi sebaran data yang lebih menyeluruh.
Arti Kuartil Ketiga (Q3) dalam Konteks Data
Kuartil ketiga (Q3) merepresentasikan nilai data yang berada di posisi 75% dari data terurut. Artinya, 75% data berada di bawah Q3. Nilai ini memberikan gambaran tentang batas atas dari 25% data tertinggi. Semakin tinggi nilai Q3, semakin tinggi rata-rata data dalam kelompok data tersebut.
Ilustrasi Pembagian Data Berdasarkan Kuartil
Bayangkan data tinggi badan siswa dalam suatu kelas. Jika Q1 = 150 cm, Q2 = 160 cm, dan Q3 = 170 cm, maka dapat disimpulkan bahwa 25% siswa memiliki tinggi badan di bawah 150 cm, 50% siswa memiliki tinggi badan di bawah 160 cm, dan 75% siswa memiliki tinggi badan di bawah 170 cm. Hal ini memberikan gambaran visual tentang sebaran tinggi badan siswa.
Analisis Penyebaran Data Berdasarkan Kuartil
Dengan menganalisis nilai Q1, Q2, dan Q3, kita dapat melihat seberapa tersebar data. Jika nilai Q1 dan Q3 berdekatan, data relatif seragam. Jika nilai Q1 dan Q3 berjauhan, data tersebar luas. Perbedaan antara Q3 dan Q1, dikenal sebagai jangkauan interkuartil (IQR), memberikan informasi tentang sebaran data di tengah-tengah data. Nilai IQR yang tinggi mengindikasikan sebaran data yang lebih luas.
Contohnya, dalam data pendapatan, jika Q1 rendah dan Q3 tinggi, maka terdapat perbedaan pendapatan yang besar di antara sebagian besar populasi. Sebaliknya, jika Q1 dan Q3 berdekatan, pendapatan cenderung terkonsentrasi pada rentang tertentu.
Penerapan Kuartil dalam Matematika: Materi Matematika Kuartil
Kuartil merupakan ukuran statistik yang membagi data terurut menjadi empat bagian yang sama besar. Pemahaman tentang penerapan kuartil sangat penting dalam analisis data, membantu kita mengidentifikasi pola dan karakteristik data dengan lebih akurat. Penerapan ini mencakup berbagai bidang, mulai dari analisis statistik deskriptif hingga inferensial.
Penggunaan Kuartil dalam Identifikasi Outlier
Kuartil dapat membantu mengidentifikasi outlier atau nilai ekstrem dalam suatu data. Outlier adalah nilai yang secara signifikan berbeda dari nilai-nilai lainnya dalam data. Dengan melihat jarak antar kuartil (IQR), kita dapat menentukan batasan nilai yang dianggap sebagai outlier. Nilai di luar batas ini kemungkinan besar merupakan outlier.
Menentukan Rentang Interkuartil (IQR)
Rentang interkuartil (IQR) adalah selisih antara kuartil ketiga (Q3) dan kuartil pertama (Q1). IQR merupakan ukuran penyebaran data yang lebih tahan terhadap outlier dibandingkan dengan rentang data keseluruhan. Nilai IQR yang kecil menunjukkan data terkonsentrasi pada suatu rentang, sementara nilai IQR yang besar mengindikasikan data tersebar lebih luas.
Misalnya, jika Q1 = 10 dan Q3 = 25, maka IQR = 25 – 10 = 15. Ini berarti 50% data berada di dalam rentang 10 hingga 25.
Studi Kasus Sederhana Analisis Data Menggunakan Kuartil
Sebuah toko ingin menganalisis penjualan produknya dalam beberapa bulan terakhir. Data penjualan (dalam ribuan rupiah) sebagai berikut: 12, 15, 18, 20, 22, 25, 28, 30, 32, 35, 40, 45. Dengan mengurutkan data, kita mendapatkan Q1 = 18,5, Q2 = 23,5, dan Q3 = 31. IQR = 31 – 18,5 = 12,5. Batas bawah untuk outlier adalah Q1 – 1,5(IQR) = 18,5 – 1,5(12,5) = 18,5 – 18,75 = -0,25.
Batas atas untuk outlier adalah Q3 + 1,5(IQR) = 31 + 1,5(12,5) = 31 + 18,75 = 49,75. Dalam data ini, tidak ada nilai yang di luar batas outlier.
Aplikasi Kuartil dalam Statistika Inferensial
Kuartil dapat digunakan dalam statistika inferensial untuk membuat estimasi tentang distribusi data populasi. Dengan mengetahui kuartil sampel, kita dapat membuat perkiraan tentang kuartil populasi. Contohnya, dalam survei kepuasan pelanggan, kuartil dapat digunakan untuk menentukan rentang nilai kepuasan yang paling sering terjadi. Hal ini dapat membantu perusahaan dalam mengidentifikasi area yang perlu ditingkatkan dalam pelayanannya.
Contoh Soal dan Latihan
Berikut disajikan beberapa contoh soal dan latihan untuk menghitung kuartil pada data tunggal dan data berkelompok. Latihan ini dirancang untuk memperkuat pemahaman Anda tentang konsep dan penerapannya.
Contoh Soal Data Tunggal
Berikut tiga contoh soal menghitung kuartil pada data tunggal:
- Contoh Soal 1: Hitunglah Q 1, Q 2, dan Q 3 dari data berikut: 5, 8, 2, 9, 6, 7, 4, 3.
- Contoh Soal 2: Tentukan nilai kuartil ketiga (Q 3) dari data: 12, 15, 18, 20, 22, 25, 28, 30.
- Contoh Soal 3: Hitunglah kuartil pertama (Q 1) dari data: 10, 12, 14, 16, 18, 20, 22, 24, 26.
Contoh Soal Data Berkelompok
Berikut dua contoh soal menghitung kuartil pada data berkelompok:
- Contoh Soal 1: Sebuah penelitian mengenai tinggi badan siswa SMP menunjukkan data sebagai berikut. Hitunglah Q 2.
Tinggi Badan (cm) Frekuensi 140 – 149 5 150 – 159 10 160 – 169 15 170 – 179 8 180 – 189 2 - Contoh Soal 2: Data nilai ulangan matematika 30 siswa disajikan dalam tabel distribusi frekuensi berikut. Tentukan nilai kuartil kedua (Q 2).
Nilai Frekuensi 40 – 49 2 50 – 59 5 60 – 69 8 70 – 79 10 80 – 89 5
Latihan Soal
Berikut beberapa latihan soal dengan variasi tingkat kesulitan:
- Latihan 1 (Mudah): Hitunglah Q 1 dan Q 3 dari data 3, 5, 7, 9, 11, 13, 15.
- Latihan 2 (Sedang): Tentukan Q 2 dari data berikut: 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30.
- Latihan 3 (Sulit): Tentukan nilai kuartil pertama (Q 1) dari data pada tabel distribusi frekuensi berikut.
Interval Frekuensi 10-19 5 20-29 8 30-39 12 40-49 10
Solusi/Jawaban
Solusi/jawaban untuk contoh soal dan latihan akan tersedia pada bagian selanjutnya.
Perbedaan Data Tunggal dan Berkelompok
| Aspek | Data Tunggal | Data Berkelompok |
|---|---|---|
| Data | Data yang disajikan secara individual | Data dikelompokkan dalam interval tertentu |
| Pengolahan | Langsung diurutkan dan dihitung kuartilnya | Perlu menghitung frekuensi kumulatif dan menentukan nilai tengah interval |
| Rumus | Rumus kuartil data tunggal | Rumus kuartil data berkelompok |
Ilustrasi Visual
Memahami distribusi data menjadi lebih mudah dengan bantuan visualisasi. Diagram kotak, histogram, scatter plot, dan diagram lingkaran dapat memberikan gambaran yang jelas tentang bagaimana data terdistribusi berdasarkan kuartil. Visualisasi ini membantu dalam menganalisis pola, tren, dan potensi outlier dalam data.
Diagram Kotak (Boxplot)
Diagram kotak, atau boxplot, merupakan visualisasi yang efektif untuk menampilkan distribusi data berdasarkan kuartil. Kotak tersebut mencakup rentang interkuartil (IQR), yang menunjukkan sebaran 50% data tengah. Garis di dalam kotak menunjukkan median. Garis-garis di luar kotak menunjukkan jangkauan data yang lebih ekstrem, yang dapat membantu mengidentifikasi outlier. Boxplot membantu membandingkan distribusi data antar kelompok atau variabel.
Histogram
Histogram menampilkan distribusi frekuensi data dalam rentang nilai tertentu. Dengan membagi data menjadi kelompok-kelompok (misalnya, berdasarkan kuartil), histogram memperlihatkan sebaran data dan frekuensi dalam setiap kuartil. Bentuk histogram dapat memberikan gambaran tentang simetri atau kemiringan distribusi data.
Grafik Scatter Plot
Scatter plot digunakan untuk melihat hubungan atau korelasi antar variabel. Dengan mempertimbangkan kuartil pada setiap variabel, kita dapat mengidentifikasi pola hubungan antara kedua variabel tersebut. Misalnya, kita bisa melihat apakah terdapat hubungan linier atau non-linier antara variabel dan bagaimana korelasinya berubah di setiap kuartil. Ini membantu dalam menganalisis hubungan dan tren dalam data.
Diagram Lingkaran
Diagram lingkaran digunakan untuk menyajikan persentase data di setiap kuartil. Diagram ini memperlihatkan proporsi data dalam setiap kuartil dengan jelas. Dengan melihat persentase, kita dapat memahami proporsi relatif data di setiap bagian dari rentang kuartil. Hal ini membantu dalam membandingkan proporsi data antar kuartil.
Pengaruh Outlier pada Posisi Kuartil
Outlier, atau data ekstrem, dapat mempengaruhi posisi kuartil. Jika outlier berada di salah satu ujung distribusi data, maka posisi kuartil akan terpengaruh. Outlier yang ekstrem dapat memindahkan median dan kuartil ke arahnya. Hal ini perlu diperhatikan dalam interpretasi hasil analisis kuartil, karena outlier dapat menghasilkan informasi yang menyesatkan.
Ringkasan Akhir
Kesimpulannya, kuartil merupakan alat penting dalam statistika untuk memahami dan menganalisis data. Dengan memahami konsep dan perhitungan kuartil, kita dapat menganalisis penyebaran data, mengidentifikasi nilai ekstrim, dan membuat interpretasi yang lebih mendalam tentang karakteristik data. Materi ini diharapkan dapat menjadi panduan yang komprehensif untuk mempelajari dan mengaplikasikan kuartil dalam berbagai situasi.